obspy.taup - Ray theoretical travel times and paths¶
| copyright: | The ObsPy Development Team (devs@obspy.org) |
|---|---|
| license: | GNU Lesser General Public License, Version 3 (https://www.gnu.org/copyleft/lesser.html) |
This package started out as port of the Java TauP Toolkit by [Crotwell1999] so please look there for more details about the algorithms used and further information. It can be used to calculate theoretical arrival times for arbitrary seismic phases in a 1D spherically symmetric background model. Furthermore it can output ray paths for all phases and derive pierce points of rays with model discontinuities.
Basic Usage¶
Let’s start by initializing a TauPyModel instance. Models can be initialized by specifying the name of a model provided by ObsPy.
>>> from obspy.taup import TauPyModel
>>> model = TauPyModel(model="iasp91")
ObsPy currently ships with the following 1D velocity models:
- 1066a, see [GilbertDziewonski1975]
- 1066b, see [GilbertDziewonski1975]
- ak135, see [KennetEngdahlBuland1995]
- ak135f, see [KennetEngdahlBuland1995], [MontagnerKennett1995], and http://rses.anu.edu.au/seismology/ak135/ak135f.html (not supported)
- ak135f_no_mud, ak135f with ak135 used above the 120-km discontinuity; see the SPECFEM3D_GLOBE manual at https://geodynamics.org/cig/software/specfem3d_globe/
- herrin, see [Herrin1968]
- iasp91, see [KennetEngdahl1991]
- jb, see [JeffreysBullen1940]
- prem, see [Dziewonski1981]
- pwdk, see [WeberDavis1990]
- sp6, see [MorelliDziewonski1993]
Custom built models can be initialized by specifying an absolute path to a model in ObsPy’s .npz model format instead of just a model name. Model initialization is a fairly expensive operation so make sure to do it only if necessary. See below for information on how to build a .npz model file.
Travel Times¶
The models’ main method is the get_travel_times() method; as the name suggests it returns travel times for the chosen phases, distance, source depth, and model. By default it returns arrivals for a number of phases.
>>> arrivals = model.get_travel_times(source_depth_in_km=55,
... distance_in_degree=67)
>>> print(arrivals)
28 arrivals
P phase arrival at 647.041 seconds
pP phase arrival at 662.233 seconds
sP phase arrival at 668.704 seconds
PcP phase arrival at 674.865 seconds
PP phase arrival at 794.992 seconds
PKiKP phase arrival at 1034.098 seconds
pPKiKP phase arrival at 1050.529 seconds
sPKiKP phase arrival at 1056.721 seconds
S phase arrival at 1176.948 seconds
pS phase arrival at 1195.508 seconds
SP phase arrival at 1196.830 seconds
sS phase arrival at 1203.129 seconds
PS phase arrival at 1205.421 seconds
SKS phase arrival at 1239.090 seconds
SKKS phase arrival at 1239.109 seconds
ScS phase arrival at 1239.512 seconds
SKiKP phase arrival at 1242.388 seconds
pSKS phase arrival at 1260.314 seconds
sSKS phase arrival at 1266.921 seconds
SS phase arrival at 1437.427 seconds
PKIKKIKP phase arrival at 1855.271 seconds
SKIKKIKP phase arrival at 2063.564 seconds
PKIKKIKS phase arrival at 2069.756 seconds
SKIKKIKS phase arrival at 2277.857 seconds
PKIKPPKIKP phase arrival at 2353.934 seconds
PKPPKP phase arrival at 2356.425 seconds
PKPPKP phase arrival at 2358.899 seconds
SKIKSSKIKS phase arrival at 3208.155 seconds
If you know which phases you are interested in, you can also specify them directly which speeds up the calculation as unnecessary phases are not calculated. Please note that it is possible to construct any phases that adhere to the naming scheme which is detailed later.
>>> arrivals = model.get_travel_times(source_depth_in_km=100,
... distance_in_degree=45,
... phase_list=["P", "PSPSPS"])
>>> print(arrivals)
3 arrivals
P phase arrival at 485.210 seconds
PSPSPS phase arrival at 4983.041 seconds
PSPSPS phase arrival at 5799.249 seconds
Each arrival is represented by an Arrival object which can be queried for various attributes.
>>> arr = arrivals[0]
>>> arr.ray_param, arr.time, arr.incident_angle
(453.7535..., 485.2100..., 24.3988...)
Ray Paths¶
To also calculate the paths travelled by the rays to the receiver, use the get_ray_paths() method.
>>> arrivals = model.get_ray_paths(500, 130)
>>> arrival = arrivals[0]
The result is a NumPy record array containing ray parameter, time, distance and depth to use however you see fit.
>>> arrival.path.dtype
dtype([('p', '<f8'), ('time', '<f8'), ('dist', '<f8'), ('depth', '<f8')])
Pierce Points¶
If you only need the pierce points of ray paths with model discontinuities, use the get_pierce_points() method which results in pierce points being stored as a record array on the arrival object.
>>> arrivals = model.get_pierce_points(500, 130)
>>> arrivals[0].pierce.dtype
dtype([('p', '<f8'), ('time', '<f8'), ('dist', '<f8'), ('depth', '<f8')])
Plotting¶
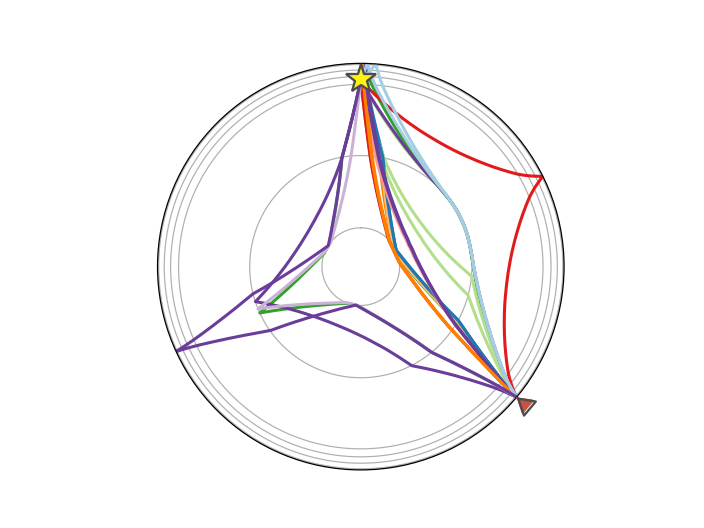
If ray paths have been calculated, they can be plotted using the Arrivals.plot_rays() method:
>>> arrivals = model.get_ray_paths(
... source_depth_in_km=500, distance_in_degree=130, phase_list=["ttbasic"])
>>> ax = arrivals.plot_rays()
(Source code, png, hires.png)
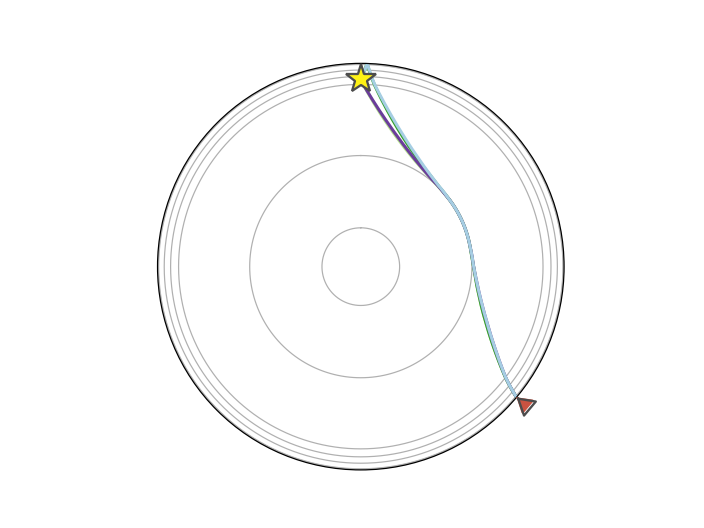
Plotting will only show the requested phases:
>>> arrivals = model.get_ray_paths(source_depth_in_km=500,
... distance_in_degree=130,
... phase_list=["Pdiff", "Sdiff",
... "pPdiff", "sSdiff"])
>>> ax = arrivals.plot_rays()
(Source code, png, hires.png)
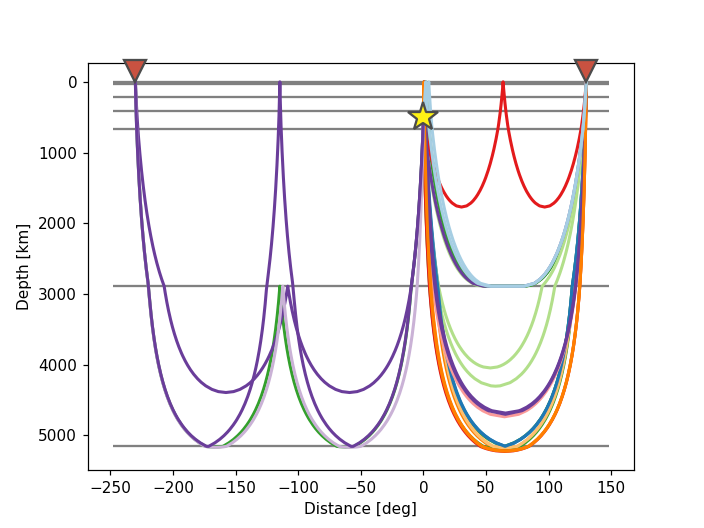
Additionally, Cartesian coordinates may be used instead of a polar grid:
>>> arrivals = model.get_ray_paths(source_depth_in_km=500,
... distance_in_degree=130,
... phase_list=["ttbasic"])
>>> ax = arrivals.plot_rays(plot_type="cartesian")
(Source code, png, hires.png)
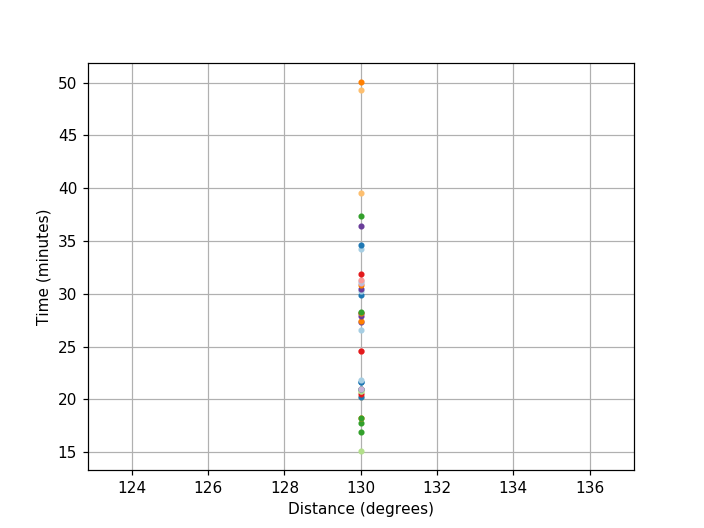
Travel times for these ray paths can be plotted using the Arrivals.plot_times() method:
>>> arrivals = model.get_ray_paths(source_depth_in_km=500,
... distance_in_degree=130)
>>> ax = arrivals.plot_times()
(Source code, png, hires.png)
Alternatively, convenience wrapper functions plot the arrival times and the ray paths for a range of epicentral distances.
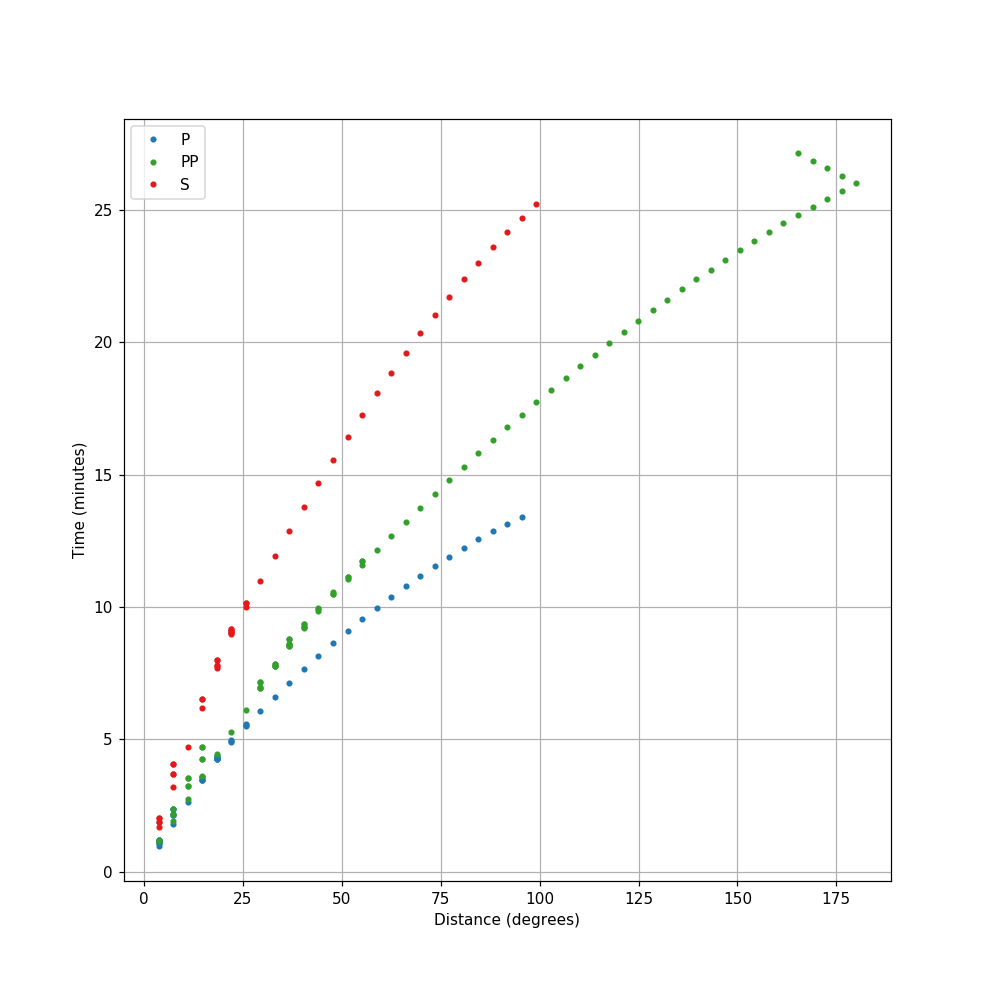
The travel times wrapper function is plot_travel_times(), creating the figure and axes first is optional to have control over e.g. figure size or subplot setup:
>>> from obspy.taup import plot_travel_times
>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots(figsize=(9, 9))
>>> ax = plot_travel_times(source_depth=10, phase_list=["P", "S", "PP"],
... ax=ax, fig=fig, verbose=True)
There was 1 epicentral distance without an arrival
(Source code, png, hires.png)
The ray path plot wrapper function is plot_ray_paths(). Again, creating the figure and axes first is optional to have control over e.g. figure size or subplot setup (note that a polar axes has to be set up when aiming to do a plot with plot_type='spherical' and a normal matplotlib axes when aiming to do a plot with plot_type='cartesian'. An error will be raised when mixing the two options):
>>> from obspy.taup import plot_ray_paths
>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots(subplot_kw=dict(projection='polar'))
>>> ax = plot_ray_paths(source_depth=100, ax=ax, fig=fig, verbose=True)
There were rays for all but the following epicentral distances:
[0.0, 360.0]
More examples of plotting may be found in the ObsPy tutorial.
Phase naming in obspy.taup¶
Note
This section is a modified copy from the Java TauP Toolkit documentation so all credit goes to the authors of that.
A major feature of obspy.taup is the implementation of a phase name parser that allows the user to define essentially arbitrary phases through a planet. Thus, obspy.taup is extremely flexible in this respect since it is not limited to a pre-defined set of phases. Phase names are not hard-coded into the software, rather the names are interpreted and the appropriate propagation path and resulting times are constructed at run time. Designing a phase-naming convention that is general enough to support arbitrary phases and easy to understand is an essential and somewhat challenging step. The rules that we have developed are described here. Most of the phases resulting from these conventions should be familiar to seismologists, e.g. pP, PP, PcS, PKiKP, etc. However, the uniqueness required for parsing results in some new names for other familiar phases.
In traditional “whole-Earth” seismology, there are 3 major interfaces: the free surface, the core-mantle boundary, and the inner-outer core boundary. Phases interacting with the core-mantle boundary and the inner core boundary are easy to describe because the symbol for the wave type changes at the boundary (i.e., the symbol P changes to K within the outer core even though the wave type is the same). Phase multiples for these interfaces and the free surface are also easy to describe because the symbols describe a unique path. The challenge begins with the description of interactions with interfaces within the crust and upper mantle. We have introduced two new symbols to existing nomenclature to provide unique descriptions of potential paths. Phase names are constructed from a sequence of symbols and numbers (with no spaces) that either describe the wave type, the interaction a wave makes with an interface, or the depth to an interface involved in an interaction.
- Symbols that describe wave-type are:
- P - compressional wave, upgoing or downgoing; in the crust or mantle, p is a strictly upgoing P-wave in the crust or mantle
- S - shear wave, upgoing or downgoing, in the crust or mantle
- s - strictly upgoing S-wave in the crust or mantle
- K - compressional wave in the outer core
- I - compressional wave in the inner core
- J - shear wave in the inner core
- Symbols that describe interactions with interfaces are:
- m - interaction with the Moho
- g appended to P or S - ray turning in the crust
- n appended to P or S - head wave along the Moho
- c - topside reflection off the core mantle boundary
- i - topside reflection off the inner core outer core boundary
- ˆ - underside reflection, used primarily for crustal and mantle interfaces
- v - topside reflection, used primarily for crustal and mantle interfaces
- diff appended to P or S - diffracted wave along the core mantle boundary
- kmps appended to a velocity - horizontal phase velocity (see 10 below)
- ed appended to P or S - an exclusively downgoing path, for a receiver below the source (see 3 below)
The characters p and s always represent up-going legs. An example is the source to surface leg of the phase pP from a source at depth. P and S can be turning waves, but always indicate downgoing waves leaving the source when they are the first symbol in a phase name. Thus, to get near-source, direct P-wave arrival times, you need to specify two phases p and P or use the “ttimes compatibility phases” described below. However, P may represent a upgoing leg in certain cases. For instance, PcP is allowed since the direction of the phase is unambiguously determined by the symbol c, but would be named Pcp by a purist using our nomenclature.
With the ability to have sources at depth, there is a need to specify the difference between a wave that is exclusively downgoing to the receiver from one that turns and is upgoing at the receiver. The suffix ed can be appended to indicate exclusively downgoing. So for a source at 10 km depth and a receiver at 20 km depth at 0 degree distance P does not have an arrival but Ped does.
Numbers, except velocities for kmps phases (see 10 below), represent depths at which interactions take place. For example, P410s represents a P-to-S conversion at a discontinuity at 410km depth. Since the S-leg is given by a lower-case symbol and no reflection indicator is included, this represents a P-wave converting to an S-wave when it hits the interface from below. The numbers given need not be the actual depth; the closest depth corresponding to a discontinuity in the model will be used. For example, if the time for P410s is requested in a model where the discontinuity was really located at 406.7 kilometers depth, the time returned would actually be for P406.7s. The code would note that this had been done. Obviously, care should be taken to ensure that there are no other discontinuities closer than the one of interest, but this approach allows generic interface names like “410” and “660” to be used without knowing the exact depth in a given model.
If a number appears between two phase legs, e.g. S410P, it represents a transmitted phase conversion, not a reflection. Thus, S410P would be a transmitted conversion from S to P at 410km depth. Whether the conversion occurs on the down-going side or up-going side is determined by the upper or lower case of the following leg. For instance, the phase S410P propagates down as an S, converts at the 410 to a P, continues down, turns as a P-wave, and propagates back across the 410 and to the surface. S410p on the other hand, propagates down as a S through the 410, turns as an S-wave, hits the 410 from the bottom, converts to a p and then goes up to the surface. In these cases, the case of the phase symbol (P vs. p) is critical because the direction of propagation (upgoing or downgoing) is not unambiguously defined elsewhere in the phase name. The importance is clear when you consider a source depth below 410 compared to above 410. For a source depth greater than 410 km, S410P technically cannot exist while S410p maintains the same path (a receiver side conversion) as it does for a source depth above the 410. The first letter can be lower case to indicate a conversion from an up-going ray, e.g., p410S is a depth phase from a source at greater than 410 kilometers depth that phase converts at the 410 discontinuity. It is strictly upgoing over its entire path, and hence could also be labeled p410s. p410S is often used to mean a reflection in the literature, but there are too many possible interactions for the phase parser to allow this. If the underside reflection is desired, use the pˆ410S notation from rule 7.
Due to the two previous rules, P410P and S410S are over specified, but still legal. They are almost equivalent to P and S, respectively, but restrict the path to phases transmitted through (turning below) the 410. This notation is useful to limit arrivals to just those that turn deeper than a discontinuity (thus avoiding travel time curve triplications), even though they have no real interaction with it.
The characters ˆ and v are new symbols introduced here to represent bottom-side and top-side reflections, respectively. They are followed by a number to represent the approximate depth of the reflection or a letter for standard discontinuities, m, c or i. Reflections from discontinuities besides the core-mantle boundary, c, or inner-core outer-core boundary, i, must use the ˆ and v notation. For instance, in the TauP convention, pˆ410S is used to describe a near-source underside reflection. Underside reflections, except at the surface (PP, sS, etc.), core-mantle boundary (PKKP, SKKKS, etc.), or outer-core-inner-core boundary (PKIIKP, SKJJKS, SKIIKS, etc.), must be specified with the ˆ notation. For example, Pˆ410P and PˆmP would both be underside reflections from the 410km discontinuity and the Moho, respectively. The phase PmP, the traditional name for a top-side reflection from the Moho discontinuity, must change names under our new convention. The new name is PvmP or Pvmp while PmP just describes a P-wave that turns beneath the Moho. The reason why the Moho must be handled differently from the core-mantle boundary is that traditional nomenclature did not introduce a phase symbol change at the Moho. Thus, while PcP makes sense since a P-wave in the core would be labeled K, PmP could have several meanings. The m symbol just allows the user to describe phases interaction with the Moho without knowing its exact depth. In all other respects, the ˆ - v nomenclature is maintained.
Currently, ˆ and v for non-standard discontinuities are allowed only in the crust and mantle. Thus there are no reflections off non-standard discontinuities within the core, (reflections such as PKKP, PKiKP and PKIIKP are still fine). There is no reason in principle to restrict reflections off discontinuities in the core, but until there is interest expressed, these phases will not be added. Also, a naming convention would have to be created since “p is to P” is not the same as “i is to I”.
Currently there is no support for PKPab, PKPbc, or PKPdf phase names. They lead to increased algorithmic complexity that at this point seems unwarranted. Currently, in regions where triplications develop, the triplicated phase will have multiple arrivals at a given distance. So, PKPab and PKPbc are both labeled just PKP while PKPdf is called PKIKP.
The symbol kmps is used to get the travel time for a specific horizontal phase velocity. For example, 2kmps represents a horizontal phase velocity of 2 kilometers per second. While the calculations for these are trivial, it is convenient to have them available to estimate surface wave travel times or to define windows of interest for given paths.
As a convenience, a ttimes phase name compatibility mode is available. So ttp gives you the phase list corresponding to P in ttimes. Similarly there are tts, ttp+, tts+, ttbasic and ttall.
Building custom models¶
Custom models can be built from .tvel and .nd files using the build_taup_model() function.
Classes & Functions¶
| TauPyModel | Representation of a seismic model and methods for ray paths through it. |
Modules¶
| c_wrappers | C wrappers for some crucial inner loops of TauPy written in C. |
| helper_classes | Holds various helper classes to keep the file number manageable. |
| ray_paths | Calculations for 3D ray paths. |
| seismic_phase | Objects and functions dealing with seismic phases. |
| slowness_layer | Functions acting on slowness layers. |
| slowness_model | Slowness model class. |
| tau_branch | Object dealing with branches in the model. |
| tau_model | Internal TauModel class. |
| taup_create | Class to create new models. |
| taup_geo | Functions to handle geographical points |
| taup_path | Ray path calculations. |
| taup_pierce | Pierce point calculations. |
| taup_time | Travel time calculations. |
| tau | High-level interface to travel-time calculation routines. |
| utils | Misc functionality. |
| velocity_layer | Functionality for dealing with a single velocity layer. |
| velocity_model | Velocity model class. |