obspy.signal.tf_misfit.plot_tf_misfits

plot_tf_misfits(st1, st2, dt=0.01, t0=0.0, fmin=1.0, fmax=10.0, nf=100, w0=6, norm='global', st2_isref=True, left=0.1, bottom=0.1, h_1=0.2, h_2=0.125, h_3=0.2, w_1=0.2, w_2=0.6, w_cb=0.01, d_cb=0.0, show=True, plot_args=['k', 'r', 'b'], ylim=0.0, clim=0.0, cmap=<matplotlib.colors.LinearSegmentedColormap object>)[source]

Plot all time frequency misfits and the time series in one plot (per component).

Parameters

  • st1 – signal 1 of two signals to compare, type numpy.ndarray with shape (number of components, number of time samples) or (number of timesamples, ) for single component data

  • st2 – signal 2 of two signals to compare, type and shape as st1

  • dt – time step between two samples in st1 and st2

  • t0 – starting time for plotting

  • fmin – minimal frequency to be analyzed

  • fmax – maximal frequency to be analyzed

  • nf – number of frequencies (will be chosen with logarithmic spacing)

  • w0 – parameter for the wavelet, tradeoff between time and frequency resolution

  • norm – ‘global’ or ‘local’ normalization of the misfit

  • st2_isref (bool) – True if st2 is a reference signal, False if none is a reference

  • left – plot distance from the left of the figure

  • bottom – plot distance from the bottom of the figure

  • h_1 – height of the signal axes

  • h_2 – height of the TEM and TPM axes

  • h_3 – height of the TFEM and TFPM axes

  • w_1 – width of the FEM and FPM axes

  • w_2 – width of the TFEM, TFPM, signal etc. axes

  • w_cb – width of the colorbar axes

  • d_cb – distance of the colorbar axes to the other axes

  • show – show figure or return

  • plot_args – list of plot arguments passed to the signal 1/2 and TEM/TPM/FEM/FPM plots

  • ylim – limits in misfit for TEM/TPM/FEM/FPM

  • clim – limits of the colorbars

  • cmap – colormap for TFEM/TFPM, either a string or matplotlib.cm.Colormap instance

Returns

If show is False, returns a matplotlib.pyplot.figure object (single component data) or a list of figure objects (multi component data)

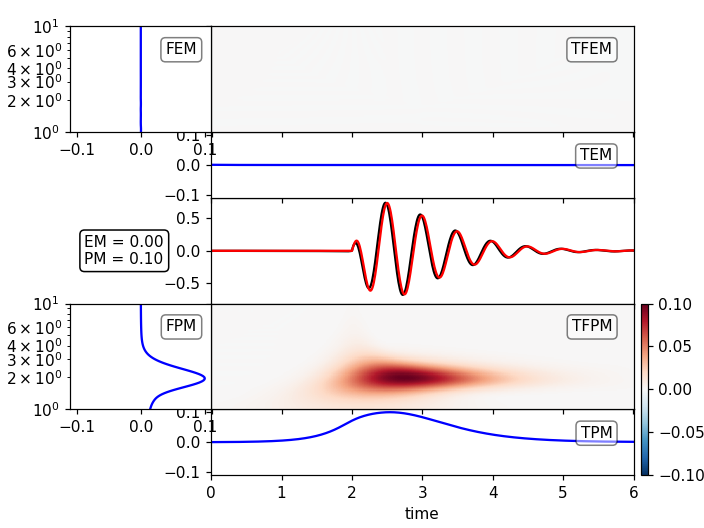
Example

For a signal with pure phase error

See also

[Kristekova2006], Fig.(4)

>>> import numpy as np
>>> from scipy.signal import hilbert
>>> tmax = 6.
>>> dt = 0.01
>>> npts = int(tmax / dt + 1)
>>> t = np.linspace(0., tmax, npts)
>>> A1 = 4.
>>> t1 = 2.
>>> f1 = 2.
>>> phi1 = 0.
>>> phase_shift = 0.1
>>> H1 = (np.sign(t - t1) + 1)/ 2
>>> st1 = (A1 * (t - t1) * np.exp(-2*(t - t1)) *
...       np.cos(2. * np.pi * f1 * (t - t1) + phi1 * np.pi) * H1)
>>> # Reference signal
>>> st2 = st1.copy()
>>> # Distorted signal:
>>> # generate analytical signal (hilbert transform) and add phase shift
>>> st1 = hilbert(st1)
>>> st1 = np.real(np.abs(st1) * np.exp((np.angle(st1) +
...                                     phase_shift * np.pi) * 1j))
>>> plot_tf_misfits(st1, st2, dt=dt, fmin=1., fmax=10.)

(Source code, png)

../../_images/obspy-signal-tf_misfit-plot_tf_misfits-1.png